Türbülans Modellemesinde Dalgaboyu Uzayı Ağları
Özgür D. GÜRCAN
LPP, CNRS, Ecole Polytechnique, Sorbonne Université, Université Paris-Saclay, Observatoire de Paris
Özet Metni İndirTürbülans, çok ölçekli doğası nedeniyle Fourier uzayında doğal olarak açık bir sistem olarak ifade edilebilir ve türbülant hareket, enerjinin veya korunan diğer bir büyüklüğün bir ölçekten diğerine transferini içerir. Türbülansın bu dalgaboyu uzayındaki kademeli aktarım imgesi, esas olarak Andrey Nikolayeviç Kolmogorov’un çalışmalarına dayanır. Enerji enjeksiyonunun büyük ölçeklerde lokalize olduğu, küçük ölçeklerde ise enerjinin dağıldığı bu yaklaşımda, arada "atalet aralığı" (inertial range) olarak adlandırılan bir ölçekler aralığı bulunur. Çok kaotik ve dengeden uzak görünen türbülant sistemler, istatistiksel anlamda büyük ölçeklerdeki enerji enjeksiyonu, büyük ölçeklerden küçük ölçeklere enerji transferi ve küçük ölçeklerdeki enerji dağılımının birbirini dengelemesi ile kararlı bir duruma gelebilir. Basit Navier-Stokes türbülansı veya daha karmaşık plazma ya da jeofizik türbülansı olsun, dalgaboyu (Fourier) uzayı ağları kullanılarak da formüle edilebilir[3, 5]. Bu ağlar, her bir noktanın diskretize edilmiş dalgaboyu uzayındaki bir dalga vektörünü temsil ettiği ve üçlü etkileşimlerin işlediği üç cisim ağlarıdır. Böyle bir üç cisim ağının bir hipergraf ile eşdeğer olduğu ve üçlemeleri de ağ elemanları haline getirerek iki parçalı (bipartite) bir ağa -yalnızca birbirleriyle etkileşime giren iki tür öğeden oluşan bir ağa- dönüştürülebileceği gösterilebilir. Türbülansın dalgaboyu uzayı ağ formülasyonu, türbülansa alternatif bir bakış açısı sağlar ve onu ağ bilimine bağlar. Denklem ve nonlineer (doğrusal olmayan) etkileşimlerin ayrılması gibi kavramsal avantajlara sahiptir. Ağ, bağlantıları aracılığıyla nonlineer etkileşimleri temsil eder ve belirli dalgaboyu türleri veya etkileşim türleri dikkate alınarak düğümler veya bağlantılar düşürülerek indirgenebilir ve bu indirgemeler, denklemlerin kendileri değiştirilmeden yapılır. Bu, denklemlerin altında yatan Hamilton yapısının değişmeden kalmasını ve dolayısıyla orijinal sistemle aynı korunum yasalarına sahip olunmasını garanti eder. Dalgaboyu uzayı ağları, benzer özelliklere sahip düğümlerin bir araya getirilmesiyle de küçültülebilir, bu durumda denklemlerin bir tür renormalizasyon ile indirgenmesi gerekir ve bunun için bazı olasılıklar tartışılmaktadır. Ağ yaklaşımı, türbülant enerji transferinde daha esnek indirgenmiş modellerinin geliştirilmesini sağlar. Küçük dünya kabuk modellerinden[4], iç içe geçmiş polyehdronlardan olusan modellere[1, 2] kadar çeşitli örnekler ve bunların etkileri tartışılacaktır.
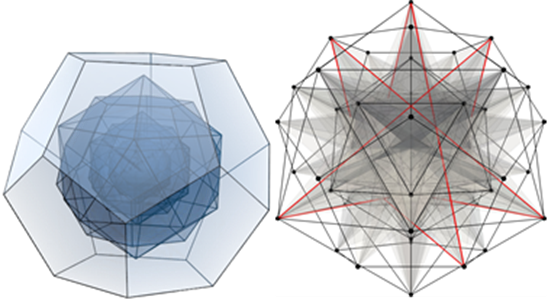
[1] Ö. D. Gürcan. Nested polyhedra model of turbulence. Phys. Rev. E, 95:063102, Jun 2017.
[2] Ö. D. Gürcan. Nested polyhedra model of isotropic magnetohydrodynamic turbulence. Phys. Rev. E, 97(6):063111, 2018.
[3] Ö. D. Gürcan. Wave-number space networks in plasma turbulence. Reviews of Modern Plasma Physics, 7:20, 2023.
[4] Özgür. D. Gürcan. Dynamical network models of the turbulent cascade. Physica D: Nonlinear Phenomena, 426:132983, 2021.
[5] Özgür. D. Gürcan, Yang Li, and Pierre Morel. Turbulence as a network of fourier modes. Mathematics, 8(4):530, Apr 2020.